Occasion for Presentation

[Presentation Title]

[Contributor List]
[Date]
[Affiliations]

Problem and opportunity: Big, dynamic data

Improved ways to observe neural network activities
  • Electrophysiology ⇒ Optogenetics
  • Calcium-sensitive fluorescent proteins
  • Voltage-sensitive fluorescent proteins
  • In vivo recording with mini-microscopes
Simultaneous recording of spiking activity from multiple neurons while the animal is freely behaving for an extended period of time
Macro-scale neural activities with human subjects
  • Electroencephalography (EEG)
  • Magnetoencephalography (MEG)
  • Functional Magnetic Resonance Imaging (fMRI)

Examples with multi-electrode arrays

Segev et al, Nat. Neurosci. 7, 1155 (2004)

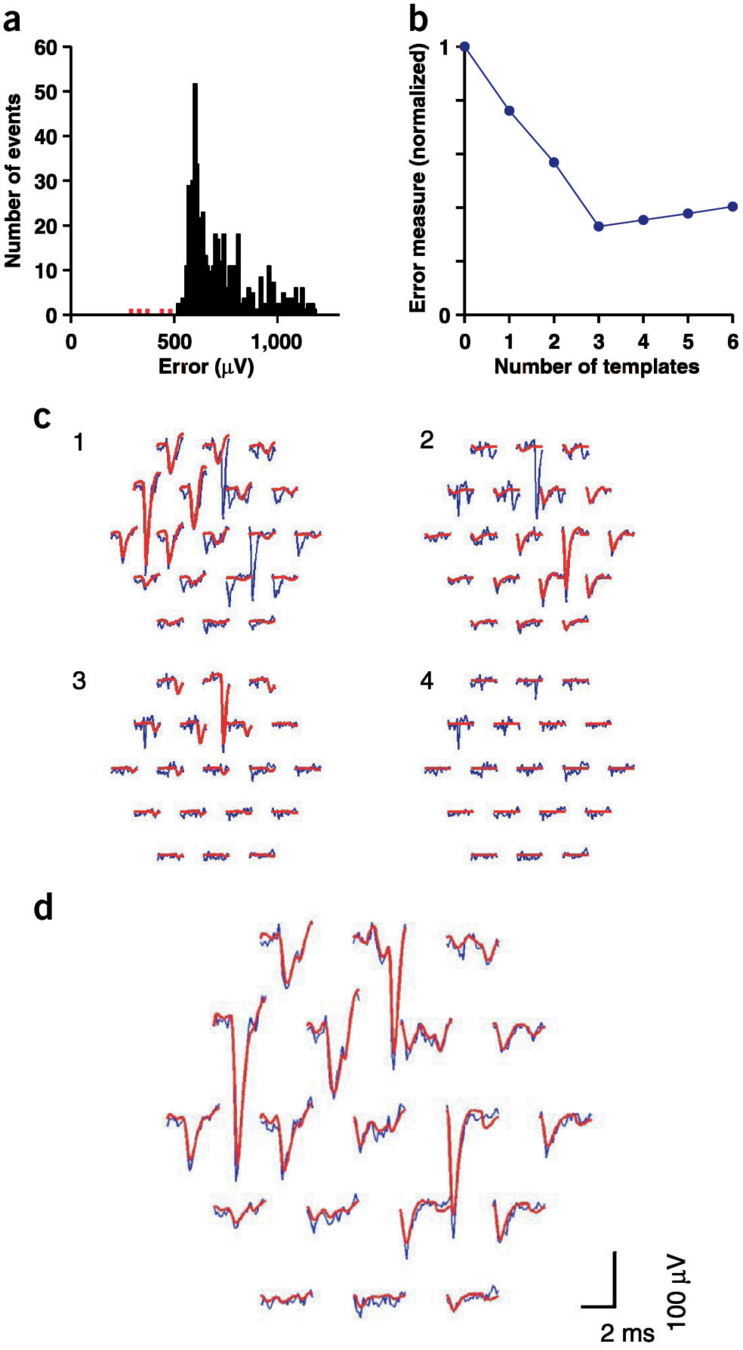
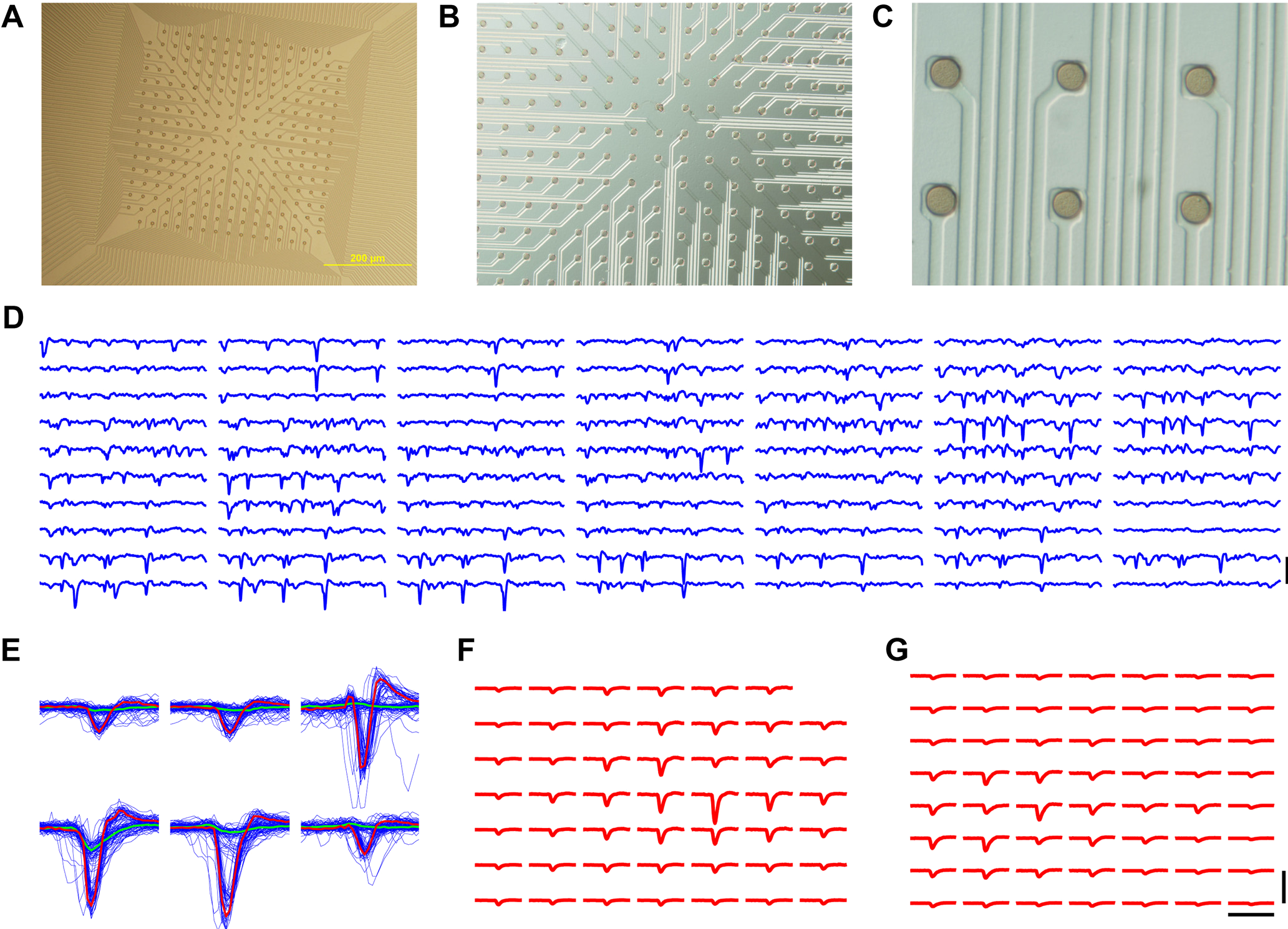
Marre et al, J. Neurosci. 32, 14859 (2012)

Example: Mouse in virtual reality

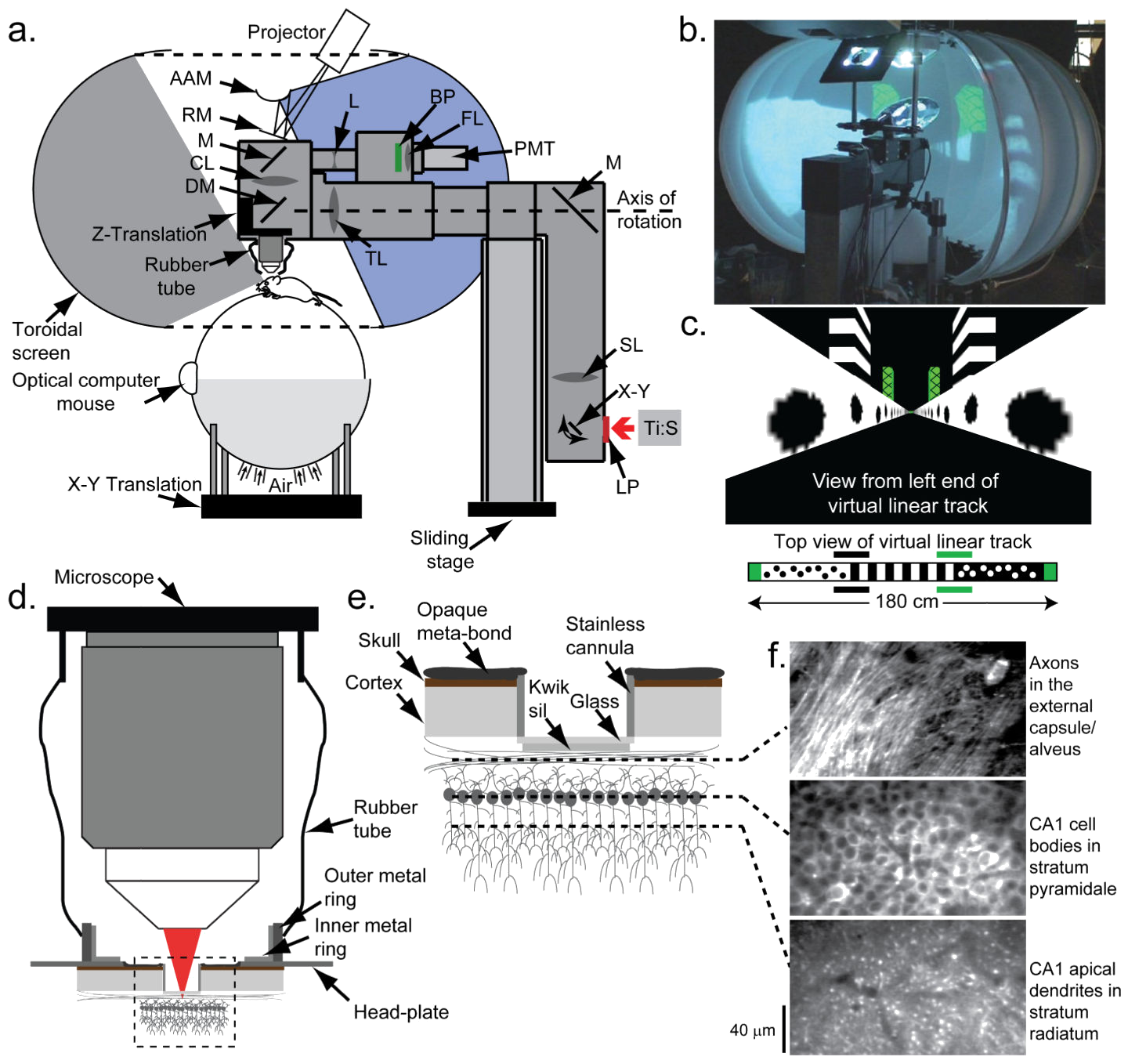
Dombeck et al, Nat. Neurosci. 13, 1433 (2010)

Mouse in a chamber

Dong Chuan Wu (吳東川)

China Medical University, Taichung

Problems with the data

  • Large number of neurons
  • Varying experimental conditions
  • Non-specific neurons
Approaches of statistical physics

Consider statistics (reduced dimensions) that are invariant under the selection of neurons, segmentation of signals, and the disturbance of the experimental conditions, while still carrying functionally relevant information.

Scope and objectives
  • Characterize the network with model thermodynamics
  • Extending the methodology to artificial network for machines of artificial intelligence
  • Characterize the learning process with states of the networks

Idea of statistical modeling

If it looks like a duck, swims like a duck, and quacks like a duck, then it probably is a duck it passes the duck's Turing test

Statistical properties

the looks, swims, and quacks

Data abstraction (segmentation)

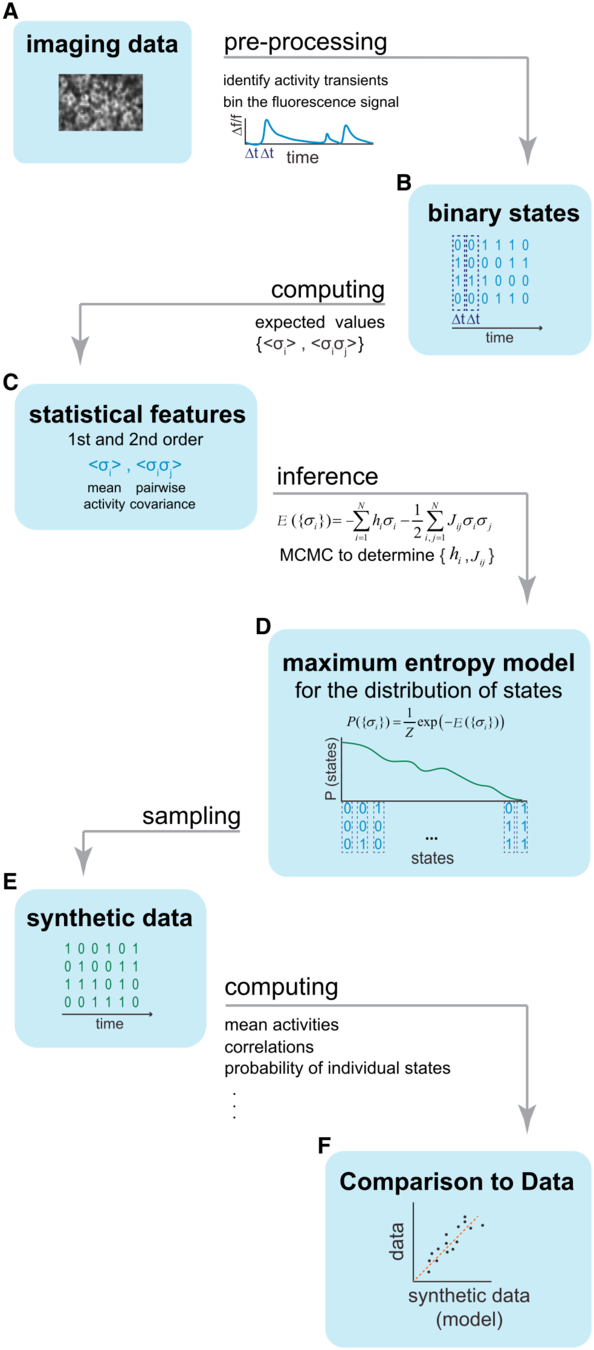
\begin{align*} m_i & = \langle \sigma_i \rangle \\ c_{i,j} & = \langle\sigma_i\sigma_j\rangle \end{align*} \begin{align*} m_i^\text{model} & \Leftrightarrow m_i^\text{data} \\ c_{i,j}^\text{model} & \Leftrightarrow c_{i,j}^\text{data} \end{align*}

Spin-glass model for pair-wise interaction

Probability distribution of states is characterized by Hamiltonian

\[ \mathcal{H} = E = - \sum_i h_i s_i - \sum_{i,j} J_{i,j} s_i s_j \]

where spins \(s=\pm1\) represent possible variations of features in a state.

Model defined by \(h_i\) and \(J_{i,j}\)

Probability of a given state \(\left\{s_i\right\}\) is given by Boltzmann distribution\[P\left(\left\{s_i\right\}\right) = Z^{-1} \exp\left(-\beta E\right)\]

From spiking to spins

\begin{align*} m_i & = \langle \sigma_i \rangle \\ C_{i,j} & = \langle \sigma_i \sigma_j \rangle \end{align*}

Spin-glass model \begin{eqnarray*}& E=-\sum_i h_i\sigma_i-\sum_{\langle i,j\rangle}J_{i,j}\sigma_i\sigma_j \\ & P\{\sigma_i\}\propto e^{-\beta E(\{s_i\})} \end{eqnarray*}

MCMC simulations

Thermodynamics

match properties

  • Phase transition
  • Criticality
  • Scaling exponents

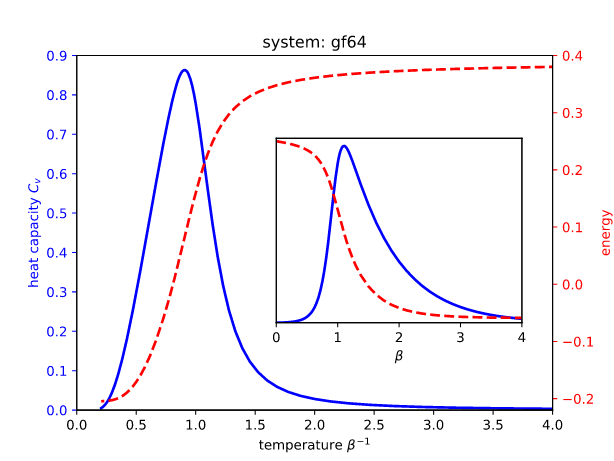
Critical state in neural networks

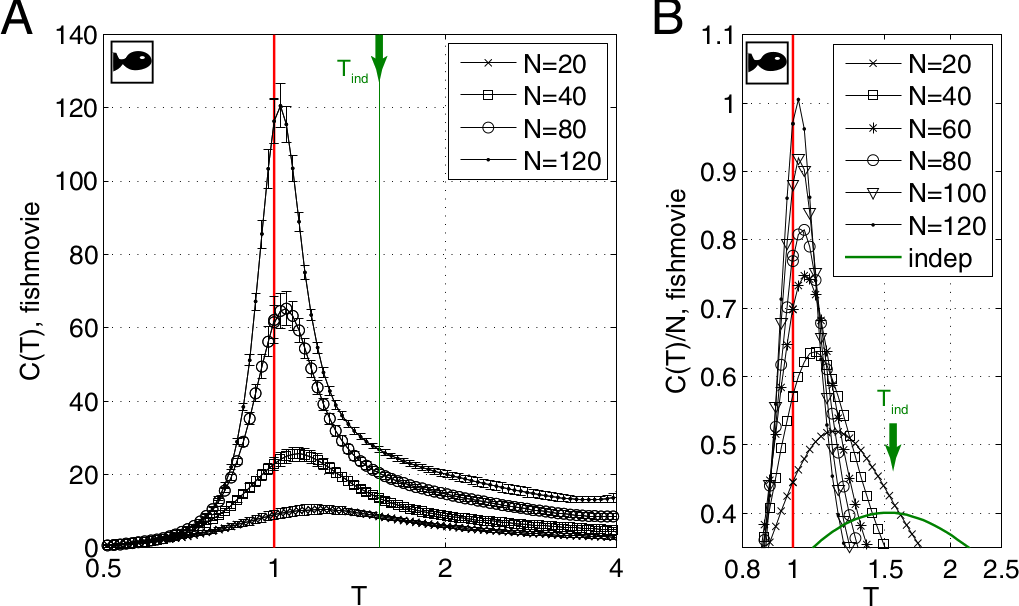
A common observation Natural systems are often poised near a critical state (peaks of $C_v$ found near $T=1$ in mapped models) See, for example,


Tkačik et al, (2015)
   

Chen et al, (2018)

Ubiquitous proximity to a critical state

Chen et al. (2022) https://doi.org/10.1016/j.cjph.2021.12.010

Similar specific heat curves for various recordings and ways of segmentation...

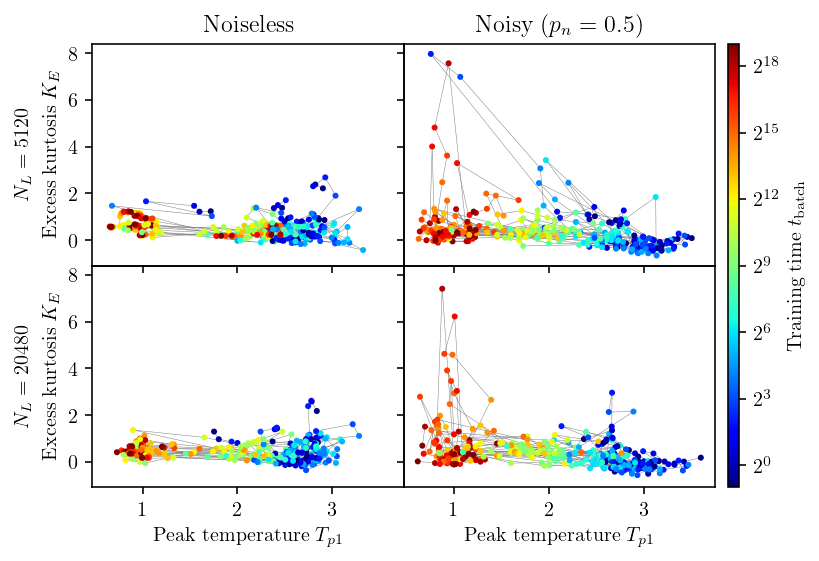
Meanings of skewness and excess kurtosis

Skewness $\gamma_1 \equiv \langle (x_i - μ)^3\rangle/\sigma^3$ measures asymmetry.

Kurtosis $K \equiv \langle (x_i - \mu)^4/\sigma^4\rangle$ measures the weight of tails.

Normal distribution $K = 3$, the excess kurtosis is defined as $$ K_E = K - 3. $$

More mouse experiment results (unpublished)

What have been learned

  • Proximity to criticality (signaled by peak in specific heat vs temperature) is robust to sampling and segmentation
  • Network structure is critical to the criticality
  • Significant non-Gaussian long-tail on positive coupling strength observed in a fraction of the model networks
  • All thresholds of coupling strengths result in networks with degree distribution consistent with Erdős–Rényi model
What we'd like to know
  • How do the neural networks get to be near a critical state?
  • Can we see the same proximity to a critical state in other networks?

Decoding the neural states of a brain

Application to artificial neural networks

MNIST dataset of handwritten digits

A typical architecture for solving MNIST

Dataset partitioning

Learning datasets are of sizes 320, 1280, 5120, and 20480 with equal number of sample images for each digits (‘0’…‘9’) chosen randomly from the original 60000 images of the MNIST training dataset. The rest of samples in the training dataset are used as the testing dataset to verify the existence of over training.

Making harder for the machines

An independent Gaussian noise is added to each pixel of an input image.

Training process under noise

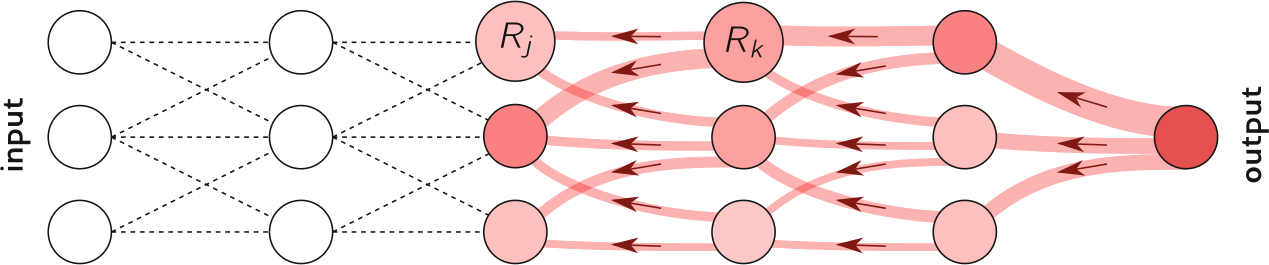
Apply statistical modeling to internal states

Treating the internal nodes just as neurons in animal brains

☆ Similar to protocol for biological neurons, the outputs of the nodes are binarized using it's STD as the threshold.

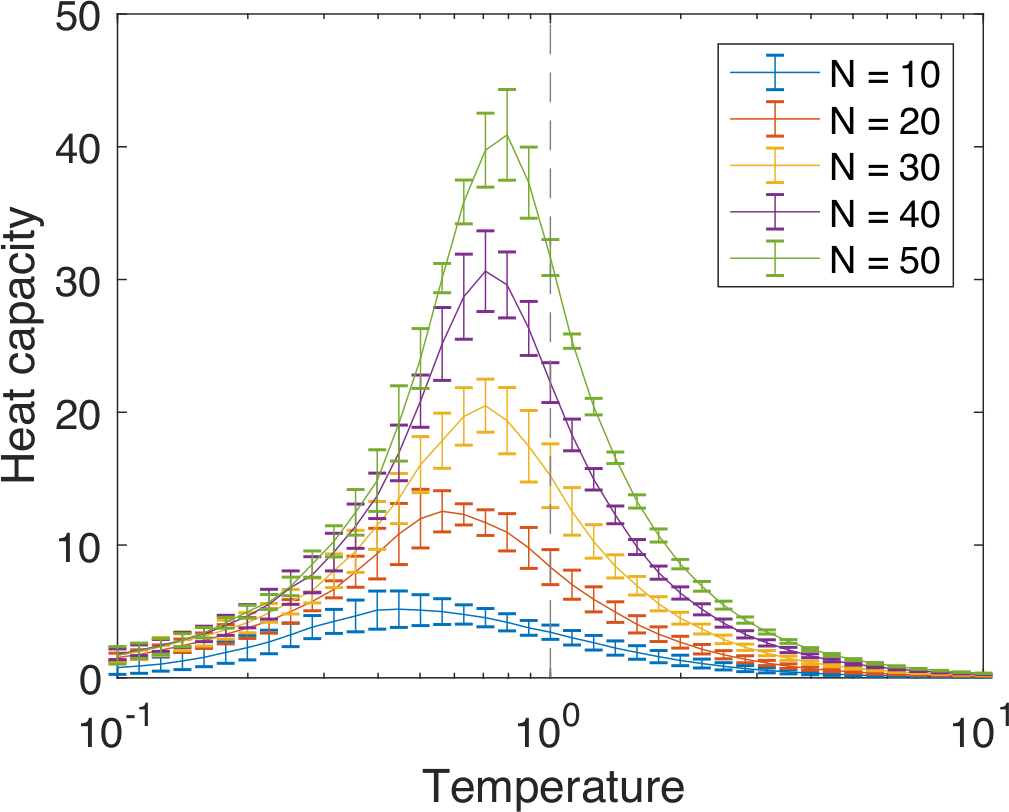
Evolution of specific heat curves

Averaged over 16 independently trained machines

Noise influences specific heat curves

Peak shift signifies change in thermodynamic properties of the model in the learning processes, with which the network approaches criticality $T_{p1}\rightarrow 1$
But, what happened to the network structure and states?

Coupling strength $J_{i,j}$ distribution

Coupling strength distribution developes significant long-tail for noisy cases when networks are optimally trained: Some links are significantly stronger than others, and likely effecting the functional dynamics of the networks

The skewness and criticality

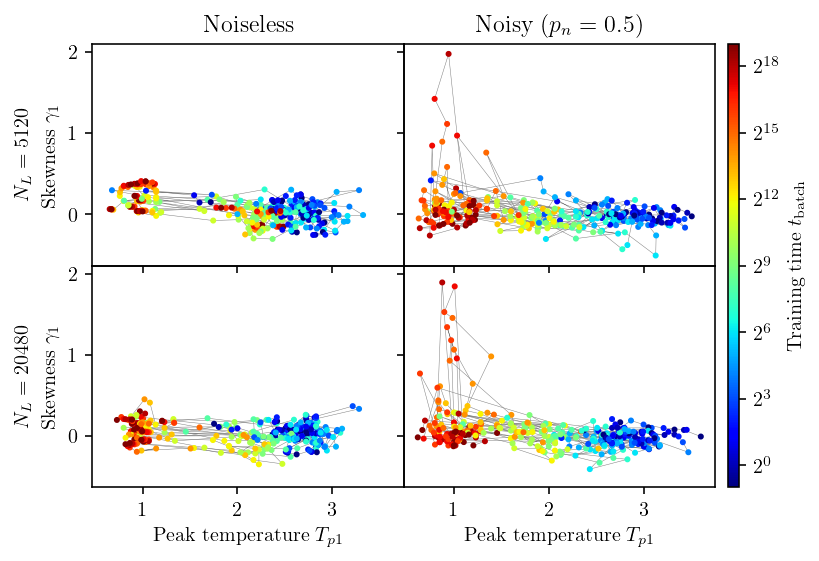
The excess kurtosis and criticality

Activation probabilities of internal nodes

Magnetization of the model spins

Activation probabilities of nodes show non-monotonic variation over the training. Without noise, activation levels after the network is optimally trained. With noise, activation keeps decreasing after a peak activation until the end of our run.

Entropy of internal state distribution

estimated through the mapped statistical model

Take $\beta$ derivative of the Helmholtz free energy $$ F\equiv U - TS = - T\ln Z $$ we find $\frac{\partial S}{\partial U} = \beta$. The energy—temperature curve, or $\beta(U)$, can be integrated from infinite temperature, $\beta = 0$, to find entropy $$ S(\beta) = S(0) + \int_{U(0)}^{U(\beta)} \beta(U) dU $$ Since all states are equally likely at $\beta=0$, the entropy is given by $S(0) = N\ln 2$.

☆ Numerical calculations in the high temperature regime are generally more stable since there are less meta-stable states to trap the simulation dynamics.

Entropy of the internal nodes

A minimum of entropy occurs around the activation peak of internal nodes before the networks are optimally trained. How are these related to the functional behavior of the networks?

Explainable artificial intelligence

Identify features contributing to the output
Layer-wise relevance propagation
Bach et al. (2015) On Pixel-Wise Explanations for Non-Linear Classifier...

→ Can be justified as a form of deep-Taylor decomposition

Montavon et al 2019

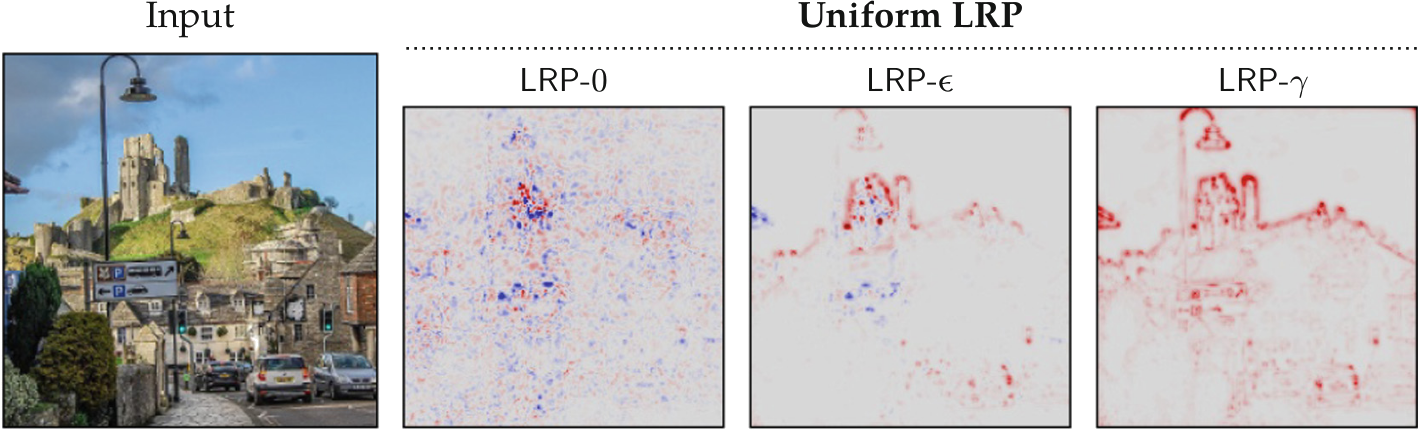
Apply LRP to the machines

the relevance heat map

Evolution of relevance map

☆ Different seeds represent independently trained networks

Quantify the clarity of relevance heat map

Contrast

Variance of the heat map pixels $R(x)$ $$ \frac{(\sum_x R(x)-\bar{R})^2}{N_\mathrm{px}} $$ where $\bar{R} = \sum_x R(x)/N_\mathrm{px}$, $N_\mathrm{px}$ is the number of pixel.

Sharpness

Mean square local gradient of the heat map $$\left|\frac{\partial R(x)}{\partial x} \right|^2 $$

☆ Both are calculated and averaged over the pixel locations $x$.

Contrast and sharpness

Qualitatively similar

☆ Shaded area represents standard deviation across the test data set.

Compare with entropy & magnetization

☆ The contrast peak strongly correlates with the entropy dip and local activation/magnetization peak.

Conclusion 1/2

  • Statistical modeling can extract information from large volume of neural data that is robust to selection of neurons and details of segmentation
  • Thermodynamics of the mapped models exhibit peaked specific heat that can separate the phase space into different regions
  • Training process in ANN results in shift and morphology change of the specific heat curves that are also influenced by different training conditions and tends to bring the network towards a critical state

Conclusion 2/2

  • For the MNIST recognizing network, training is seen fall into an earlier stage with decreasing entropy of network states and increasing contrast of relevance heat map and a later stage with increasing entropy and decreasing contrast.
  • The two stages are separated by a local peak in the activation level of the neurons or the magnetization of the model spins.

Thank you for your attention!