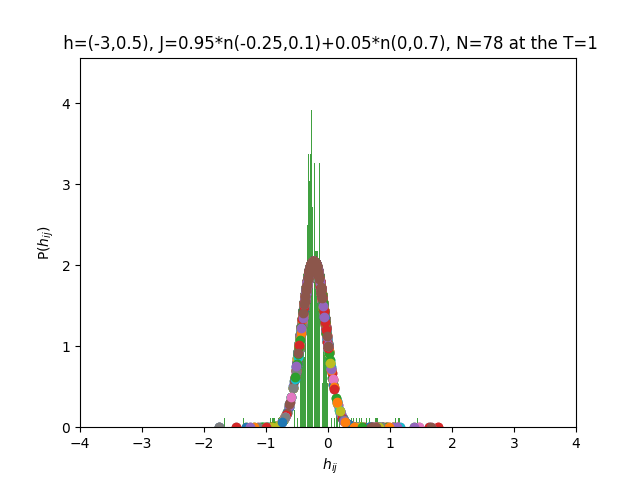
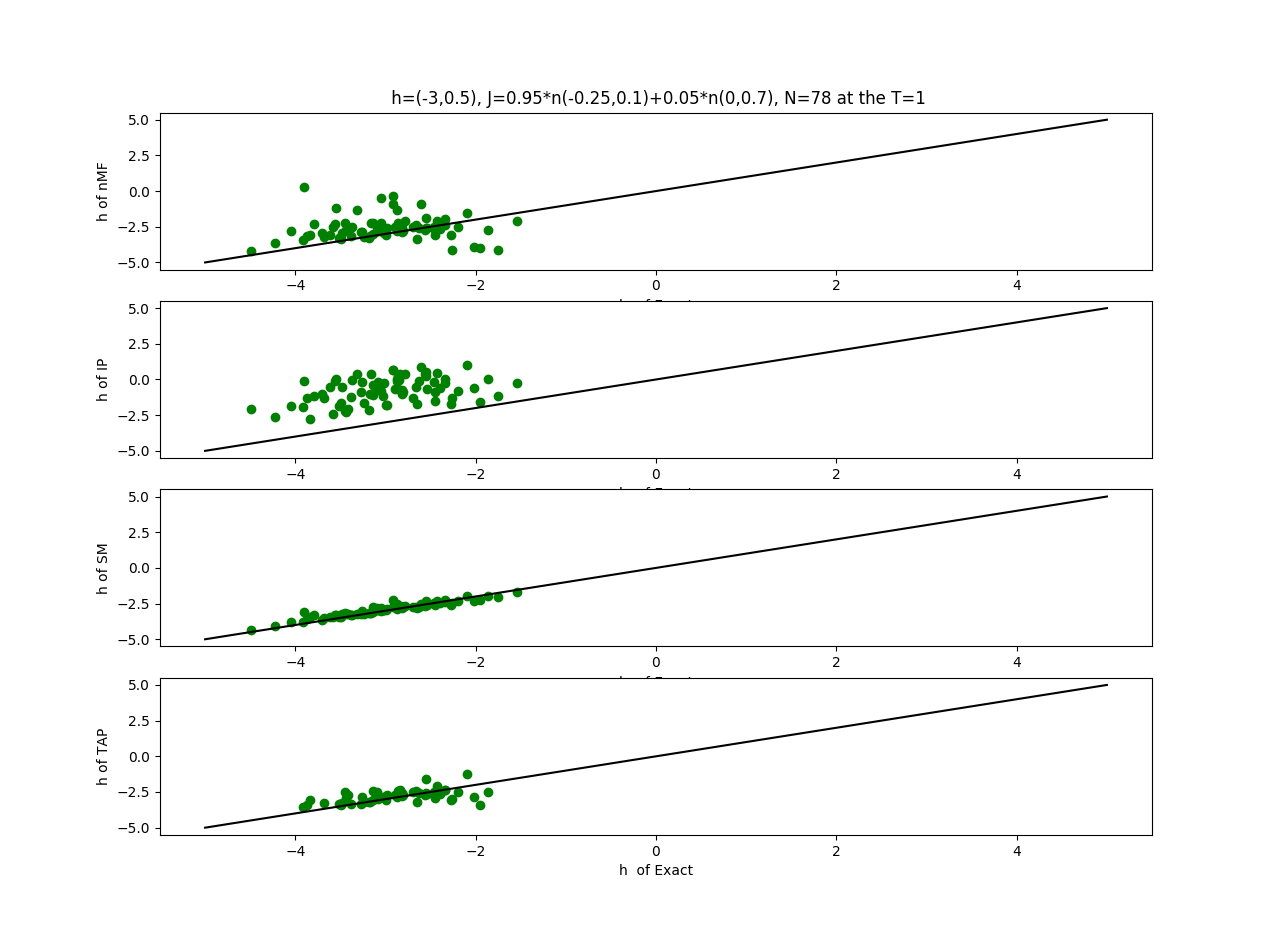
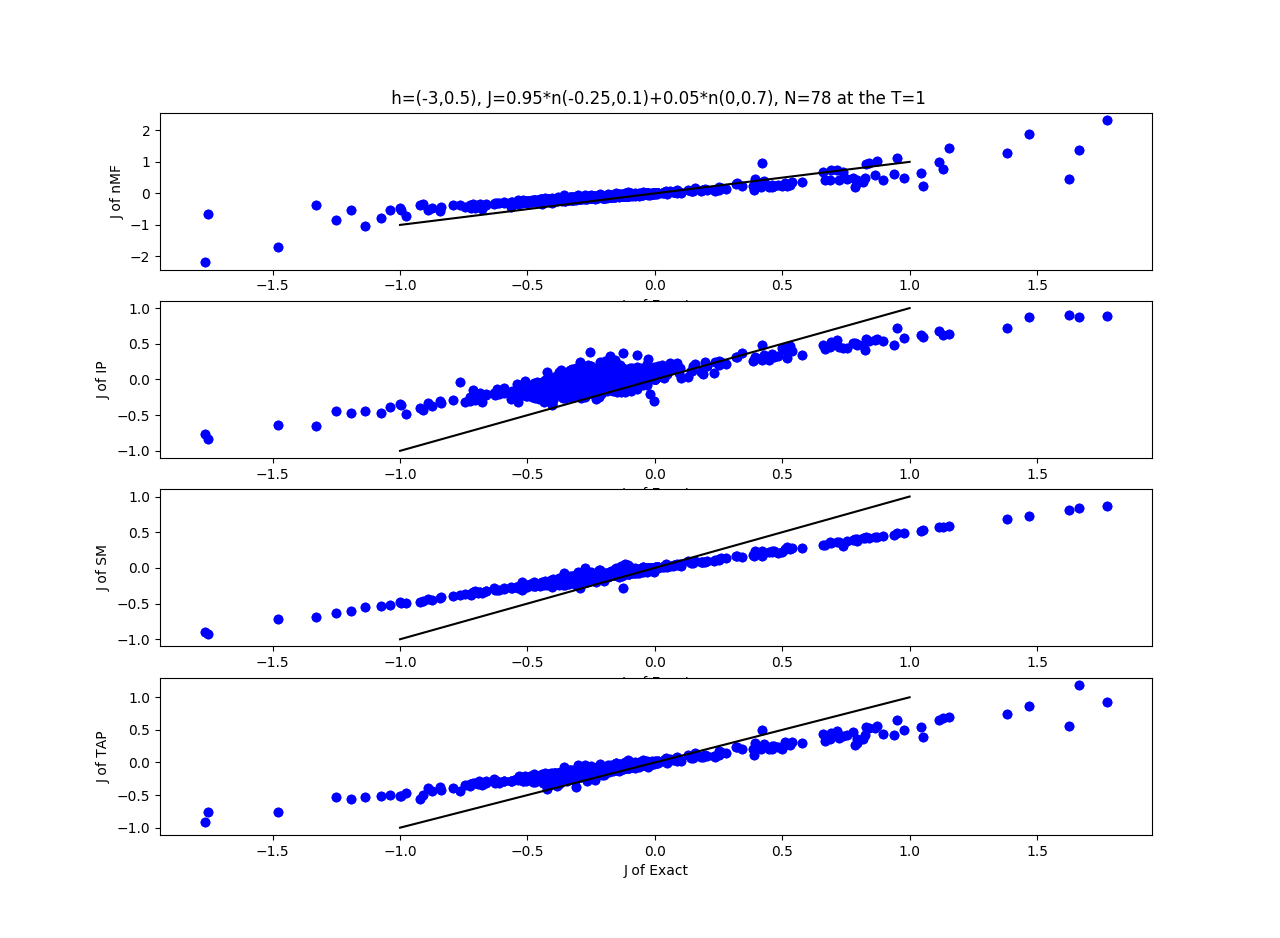
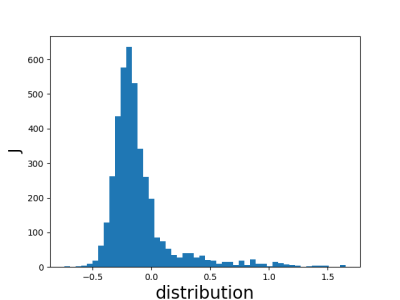
7.19.18 Inverse Problem
The mean field theory (nMF):
$\mathbf{J}^\text{nMF}=-\mathbf{C}^{-1}, (i \neq j) $,
$h_{i}^\text{nMF}=\tanh^{-1}\left< s_{i} \right>-\sum_{j=1}^{N} J{ij}^\text{nMF}\left< s_{j} \right> $ .
The independent-pair theory (IP):
$J_{ij}^\text{pair}=0.25*\ln\left[ \frac{(1+m_{i}+m_{j}+C_{ij}^{*}) (1-m_{i}-m_{j}+C_{ij}^{*})} {(1-m_{i}+m_{j}-C_{ij}^{*})(1+m_{i}-m_{j}-C_{ij}^{*})} \right]$, with $C_{ij}^{*}=C_{ij}+m_{i}m_{j} , (i \neq j)$
$h_{i}^\text{pair}=0.5*\ln\left( \frac{1+m_{i}} {1-m_{i}} \right)-\sum_{j=1}^{N} J_{ij}^\text{pair} m_{j}$.
The Thouless-Anderson-Palmer theory (TAP):
$\mathbf{C}^{-1}+J_{ij}^\text{TAP}+2(J_{ij}^\text{TAP})^{2}m_{i}m_{j}=0 , (i \neq j)$
$h_{i}^\text{TAP}=h_{i}^\text{nMF}-m_{i}\sum_{i=1}^{N} (J_{ij}^\text{TAP})^{2} (1-m_{j})^{2}$.
The Sessak and Monasson theory (SM):
$J_{ij}^\text{SM}=J_{ij}^\text{nMF}+J_{ij}^\text{pair}-\frac{C_{ij}}{(1-m_{i}^{2})(1-m_{j}^{2})-C_{ij}^{2}} , (i \neq j)$
$h_{i}^\text{SM}=0.5*\ln\left( \frac{1+m_{i}} {1-m_{i}} \right)-\sum_{j=1}^{N} J_{ij}^\text{SM} m_{j}$.
The coefficient of $R^{2}$ is:
$R^{2}=1-\frac{\sum_{ij} \left(J_{ij}^{\text{approx}}-J_{ij}^{\text{Exact}} \right)^{2} }{\sum_{ij} \left(J_{ij}^{\text{Exact}}-J_{ij}^{\text{$\overline{Exact}$}} \right)^{2}}$ , with
The rms error is: $\sqrt{\frac{1}{N(N-1)} \sum_{i \neq j} (J_{ij}^\text{approx}-J_{ij}^\text{Exact})^{2} }$.
7.24.18 Inverse Problem
| h:n(0.0,0.07) & J:n(0.0,0.07), n=200 at T=1 | $\sqrt{200}$ |
|---|---|
| h:n(0.0,0.08) & J:n(0.0,0.08), n=150 at T=1 | $\sqrt{150}$ |
| h:n(0.0,0.1) & J:n(0.0,0.10) , n=100 at T=1 | $\sqrt{100}$ |
| h:n(0.0,0.14) & J:n(0.0,0.14), n=50 at T=1 | $\sqrt{50} $ |
| h:n(0.0,0.22) & J:n(0.0,0.22), n=20 at T=1 | $\sqrt{20} $ |
We set the mean equal to zero and the variance of normal distribution of h and J from $\frac{1}{\sqrt{200}}$: $\frac{1}{\sqrt{150}}$: $\frac{1}{\sqrt{100}}$:$\frac{1}{\sqrt{50}}$:$\frac{1}{\sqrt{20}} \approx 0.07 : 0.08 : 0.1 : 0.14 : 0.22 $.
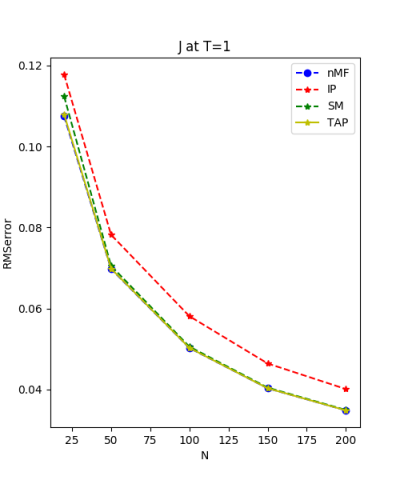
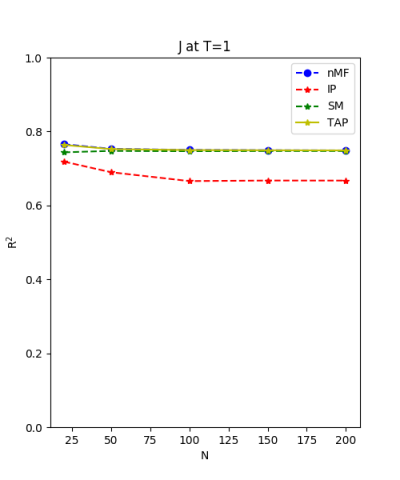
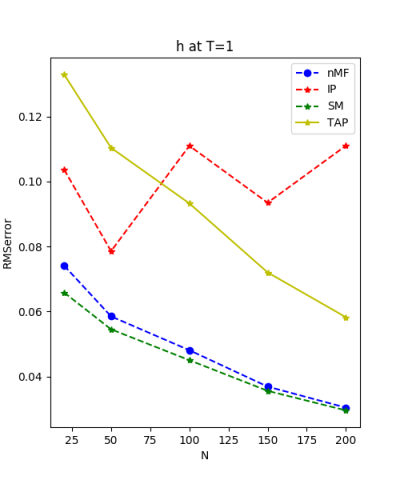
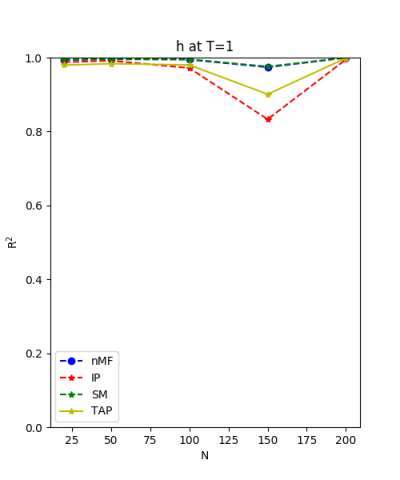
We use the normal distribution of h and J to get the coefficients of $R^{2}$ and the RMSerror at T=1.
7.24.18 DATA of Inverse Problem
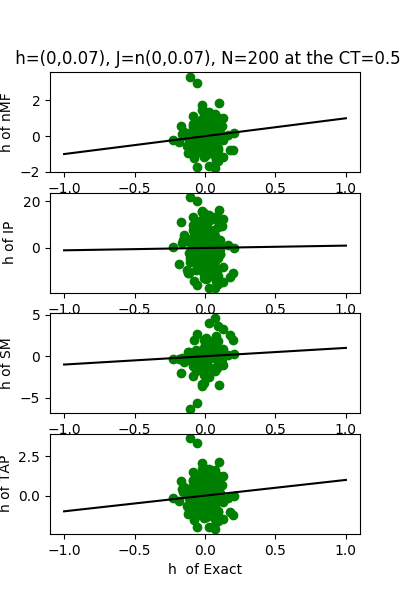
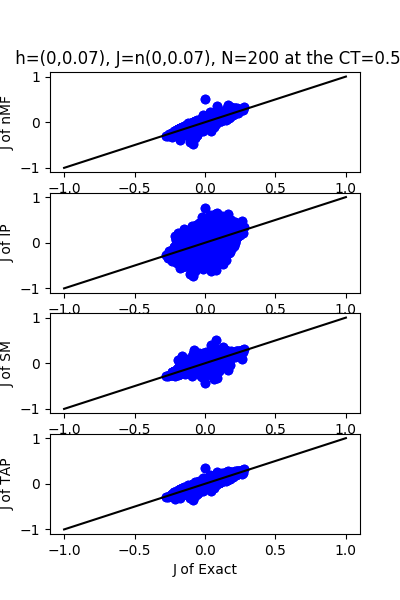
| J:n(0.0,0.07) ,n=200 at CT=0.5 | rms error | $R^{2}$ | h:n(0.0,0.07) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.01 | 0.96 | 0.88 | 0.67 | |
| IP | 0.11 | -1.85 | 10.41 | -43.71 | |
| SM | 0.02 | 0.89 | 1.57 | -0.02 | |
| TAP | 0.01 | 0.97 | 1.11 | 0.49 |
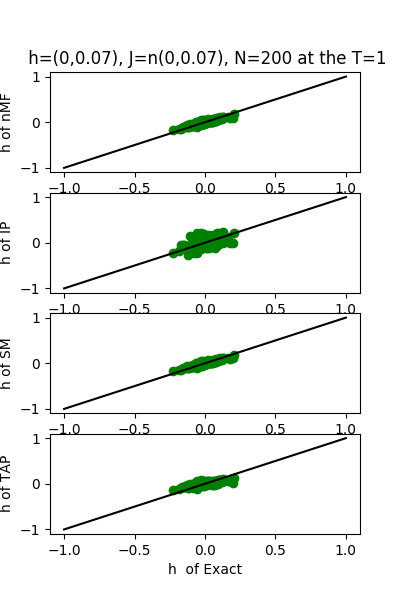
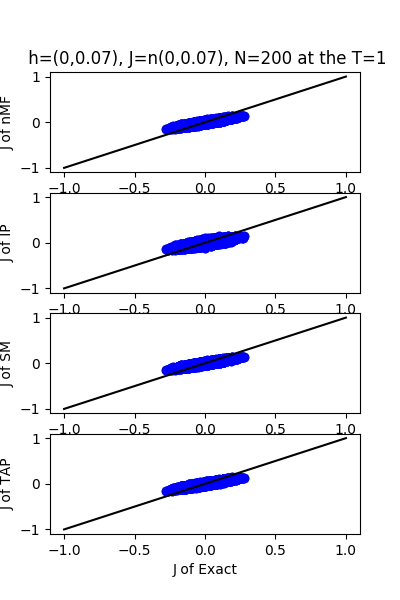
| J:n(0.0,0.07) ,n=200 at T=1.0 | rms error | $R^{2}$ | h:n(0.0,0.07) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.03 | 0.74 | 0.03 | 0.99 | |
| IP | 0.04 | 0.66 | 0.11 | 0.99 | |
| SM | 0.03 | 0.74 | 0.02 | 0.99 | |
| TAP | 0.03 | 0.74 | 0.05 | 0.99 |
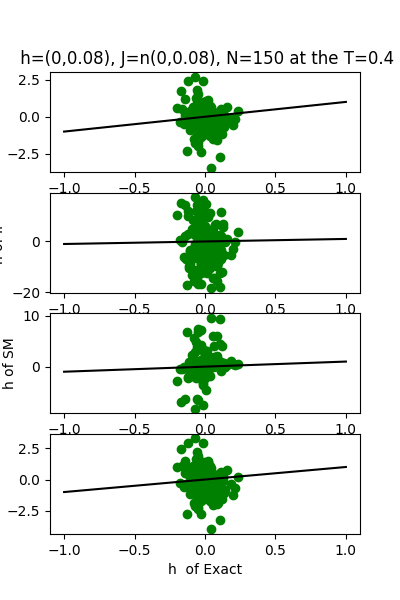
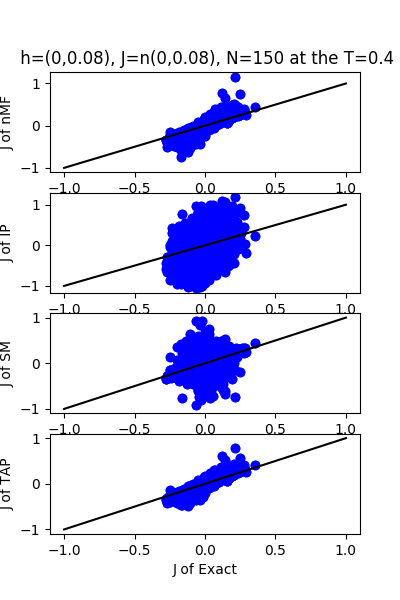
| J:n(0.0,0.08) ,n=150 at CT=0.4 | rms error | $R^{2}$ | h:n(0.0,0.08) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.03 | 0.76 | 1.28 | -30.39 | |
| IP | 0.24 | -7.94 | 12.13 | -2810.72 | |
| SM | 0.07 | 0.11 | 3.75 | -268.62 | |
| TAP | 0.03 | 0.82 | 1.67 | -52.67 |
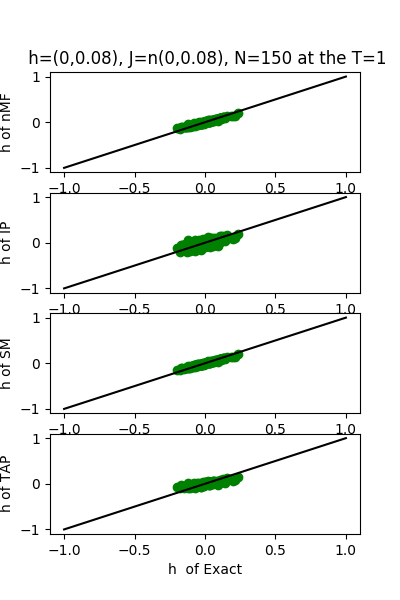
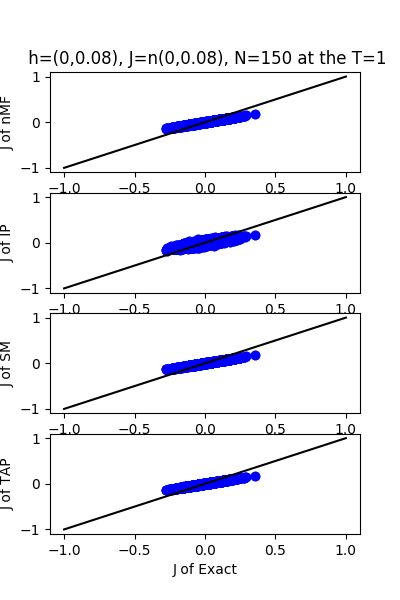
| J:n(0.0,0.08) ,n=150 at T=1 | rms error | $R^{2}$ | h:n(0.0,0.08) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.04 | 0.74 | 0.03 | 0.97 | |
| IP | 0.04 | 0.66 | 0.09 | 0.83 | |
| SM | 0.04 | 0.74 | 0.03 | 0.97 | |
| TAP | 0.04 | 0.74 | 0.07 | 0.90 |
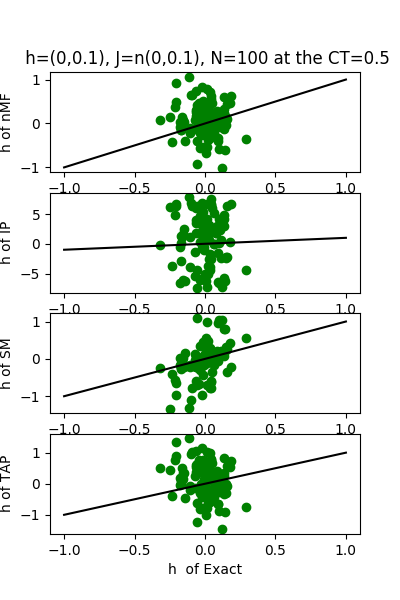
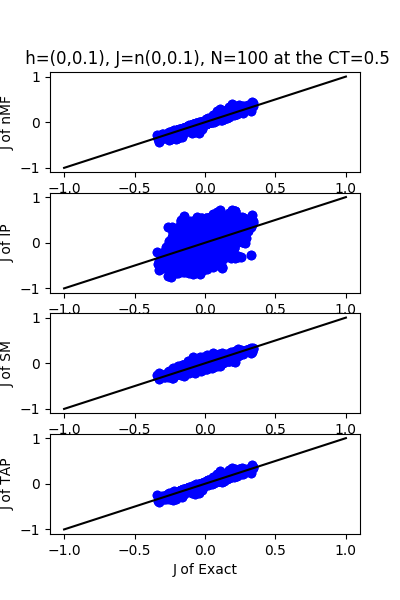
| J:n(0.0,0.1) ,n=100 at CT=0.5 | rms error | $R^{2}$ | h:n(0.0,0.1) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.01 | 0.96 | 0.59 | 0.18 | |
| IP | 0.20 | -2.96 | 6.28 | -89.71 | |
| SM | 0.02 | 0.92 | 0.60 | 0.16 | |
| TAP | 0.01 | 0.97 | 0.89 | -0.84 |
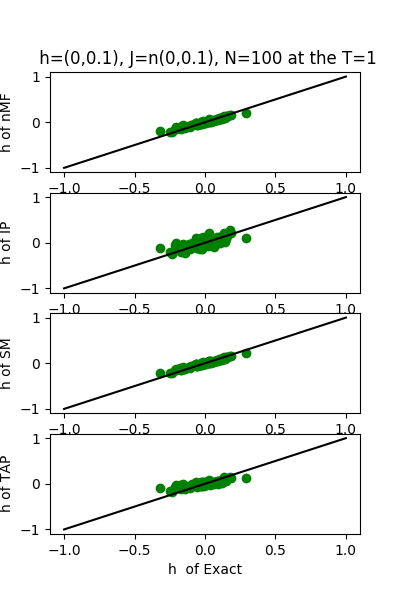
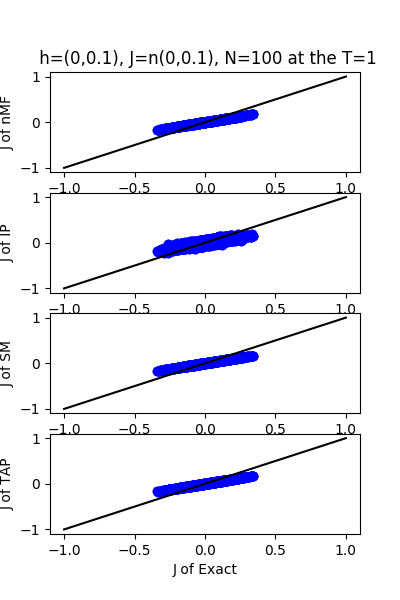
| J:n(0.0,0.1) ,n=100 at T=1 | rms error | $R^{2}$ | h:n(0.0,0.1) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.05 | 0.75 | 0.04 | 0.99 | |
| IP | 0.05 | 0.66 | 0.11 | 0.97 | |
| SM | 0.05 | 0.74 | 0.04 | 0.99 | |
| TAP | 0.05 | 0.74 | 0.09 | 0.98 |
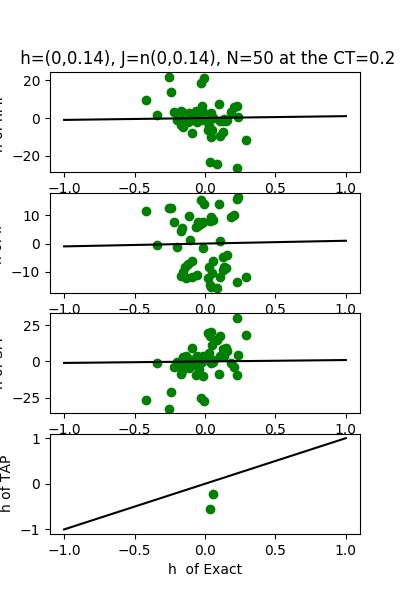
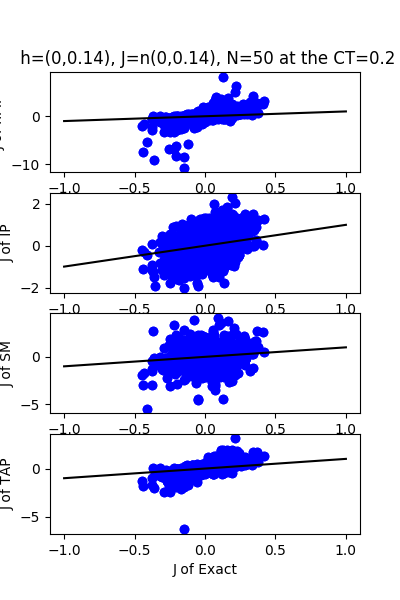
| J:n(0.0,0.14) ,n=50 at CT=0.2 | rms error | $R^{2}$ | h:n(0.0,0.14) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.33 | -50.21 | 7.59 | -77.94 | |
| IP | 0.20 | -17.71 | 8.27 | -92.61 | |
| SM | 0.27 | -34.67 | 10.06 | -137.77 | |
| TAP | 0.04 | -0.04 | 0.12 | 0.97 |
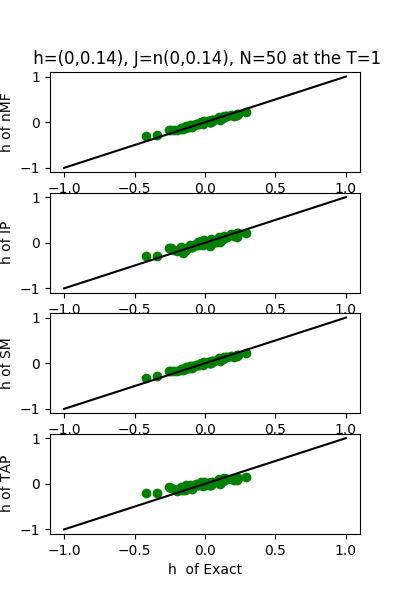
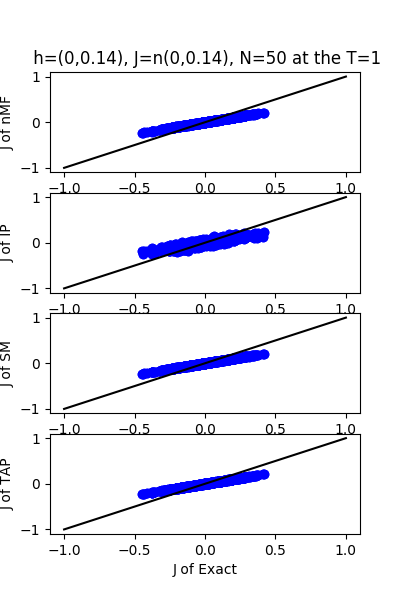
| J:n(0.0,0.14) ,n=50 at T=1 | rms error | $R^{2}$ | h:n(0.0,0.14) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.06 | 0.75 | 0.05 | 0.99 | |
| IP | 0.07 | 0.68 | 0.07 | 0.99 | |
| SM | 0.07 | 0.74 | 0.05 | 0.99 | |
| TAP | 0.06 | 0.75 | 0.11 | 0.98 |
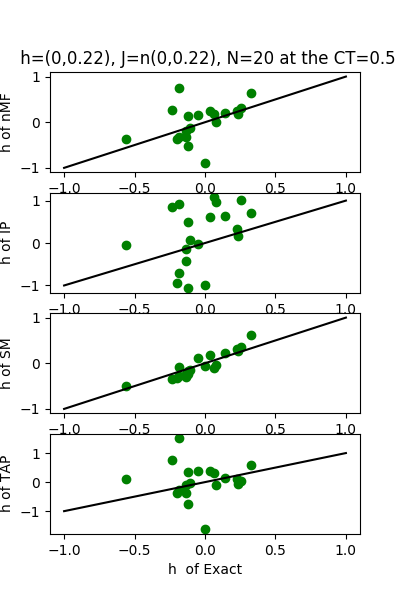
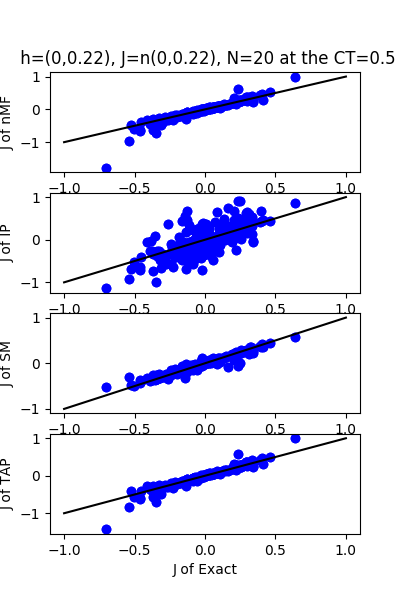
| J:n(0.0,0.22) ,n=20 at CT=0.5 | rms error | $R^{2}$ | h:n(0.0,0.22) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.10 | 0.76 | 0.49 | 0.71 | |
| IP | 0.26 | -0.42 | 0.94 | -0.03 | |
| SM | 0.05 | 0.93 | 0.17 | 0.96 | |
| TAP | 0.08 | 0.85 | 0.91 | 0.03 |
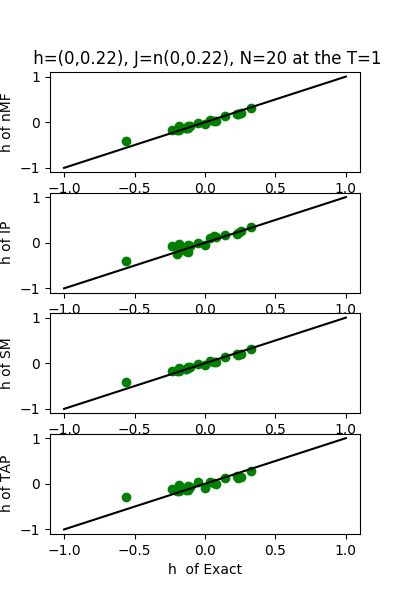
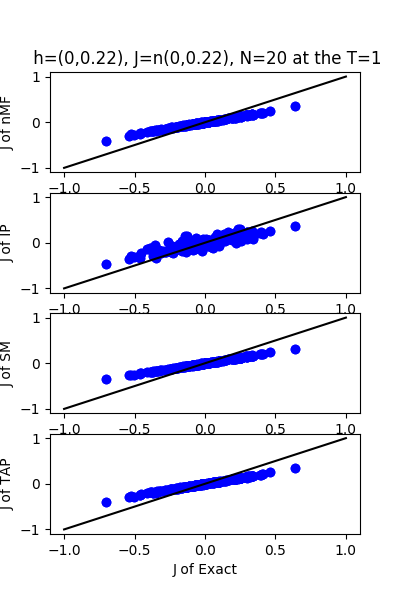
| J:n(0.0,0.22) ,n=20 at T=1 | rms error | $R^{2}$ | h:n(0.0,0.22) | rms error | $R^{2}$ |
|---|---|---|---|---|---|
| nMf | 0.10 | 0.76 | 0.07 | 0.99 | |
| IP | 0.11 | 0.71 | 0.10 | 0.98 | |
| SM | 0.11 | 0.74 | 0.06 | 0.99 | |
| TAP | 0.10 | 0.76 | 0.13 | 0.97 |
7.30.18 DATA of Inverse Problem
11-24-18 Gaussian in spins(-1,1) distributions
We consider the cases in the beta=1.0.
The external fields are h~n(0.1,0.1)
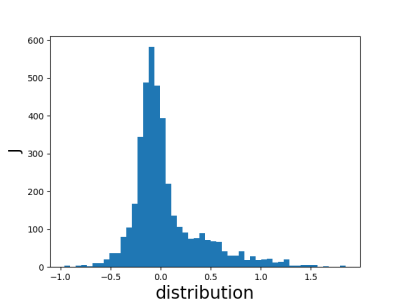
The coupling distributions are case 1: J~ 0.8*n(-0.2,0.1) +0.1*n(0,0.2)+0.1*n(0.5,0.5)
case2: J~ 0.5*n(-0.1,0.1) +0.3*n(0,0.3)+0.2*n(0.5,0.5)
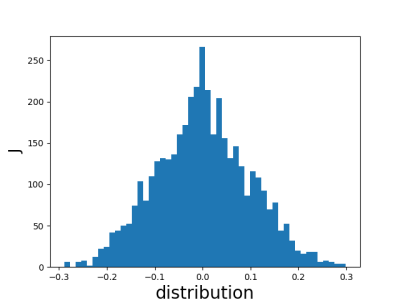
case3: J~ 1*n(0,0.1)
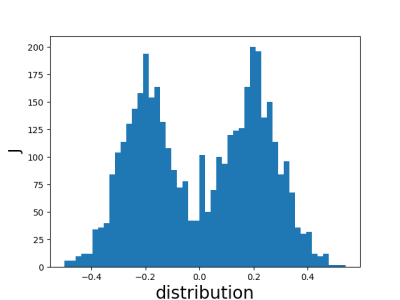
case4: J~ 0.5*n(-0.2,0.1) +0.5*n(0.2,0.1)
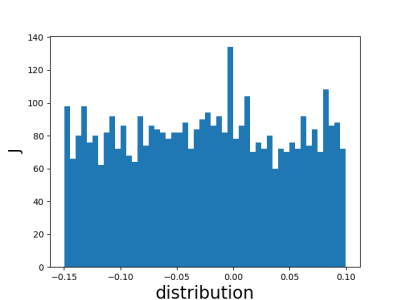
case5: J~ 1*uniform(-0.15,0.1)